数理最適化で数独を解いてみた（PuLP編）

こんにちは、@yshr10icです。

2022年頃から個人的に数理最適化を勉強しています。定式化された問題に対して、PuLPやGoogle OR-Toolsを使ってなんとなく実装することができるようになりましたが、自分自身で定式化するところはまだまだできるレベルではありません。

そこで2023年は「数理最適化をある程度使いこなせるようになる」ことを目標に掲げ、身の回りにあることを定式化・実装していくことにしました。2023年の目標については以下のブログに記載しています。

2023年の目標こんにちは、@yshr10icです。 2023年になって1週間となりました。 2023年の目標を書いておこうかと思います。 ...

そうは言っても、身の回りにあることで数理最適化で定式化できる問題ってなんだよと思っていたところ、Twitterでイラストロジックなるものを見て、挑戦してみました。

今年のイラストロジックです！
割と簡単なはず！ pic.twitter.com/UVROsiakaG
— クルトン (@kuruton456) December 31, 2022

先日Twitterでイラストロジックを見て、これ数理最適化で解けるんじゃね？と思ったので、解いてみることにした
まずは問題を取ってくるところまでできたので、これから定式化してみる pic.twitter.com/XrGjTSdlbt
— yshr10ic (@yshr_10ic) January 3, 2023

挑戦してみましたが、挫折しました。

いきなりイラストロジックは難しかったです。

まずはイラストロジックより制約条件が簡単で似たような問題である数独に挑戦することにしました。

イラストロジックを数理最適化で解くのは自分にはまだ早かったので、まずは数独から解くことにした。
いい練習になった。 pic.twitter.com/06hckCiKcx
— yshr10ic (@yshr_10ic) January 7, 2023

数理最適化で数独を解くことができたので、簡単にその内容をまとめようと思います。

Contents

今回解く数独の定義
定式化
実装
まとめ
- 数理最適化を勉強するのにおすすめな書籍

今回解く数独の定義

今回試しに解いてみる数独の問題は以下です。

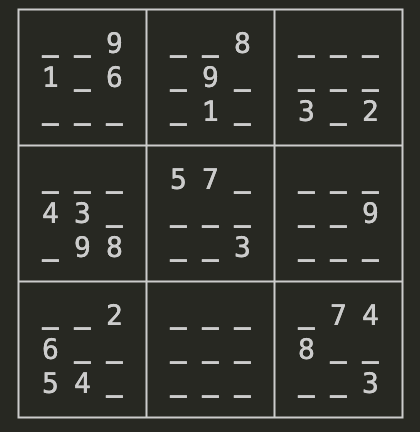
定式化

数理最適化では、決定変数、制約条件、目的関数を定義する必要があります。それぞれ定義していきます。

決定変数

9×9のそれぞれのマスに対して1〜9の数字が入るかどうかのバイナリ変数を用意します。

行集合を $\text{rows} \in \{ 1, 2, \cdots, 9 \}$ 、列集合を $\text{cols} \in \{ 1, 2, \cdots, 9 \}$ 、それぞれのセルに入る番号の集合を $\text{nums} \in \{ 1, 2, \cdots, 9 \}$ とし、それぞれのインデックスを $\text{row}, \text{col}, \text{num}$ とします。

$\text{row}$ 行目、 $\text{col}$ 列の番号が $\text{num}$ のバイナリ変数を $x_{\text{row}, \text{col}, \text{num}}$ とします。

この時、問題の2行3列目の値は6となっているため、 $x_{2,3,6}=1$ となり、 $\text{num} \in \{ 1, 2, 3, 4, 5, 7, 8, 9 \}$ の $x_{2,3,\text{num}}=0$ となります。

決定変数ではないですが、もともと埋まっている数字を $\text{hint}_{\text{row}, \text{col}} = \text{num}$ とします。

制約条件

制約条件①：各マスには必ず1〜9のいずれかの数字が入る

$\sum _{\text{num} \in \text{nums}} x_{\text{row}, \text{col}, \text{num}} = 1, \hspace{10pt} \forall \text{row} \in \text{rows}, \text{col} \in \text{cols}$

制約条件②：行方向に見た時に、同じ数字は入らない

$\sum _{\text{col} \in \text{cols}} x_{\text{row}, \text{col}, \text{num}} = 1, \hspace{10pt} \forall \text{row} \in \text{rows}, \text{num} \in \text{nums}$

制約条件③：列方向に見た時に、同じ数字は入らない

$\sum _{\text{row} \in \text{rows}} x_{\text{row}, \text{col}, \text{num}} = 1, \hspace{10pt} \forall \text{col} \in \text{cols}, \text{num} \in \text{nums}$

制約条件④：3×3のマスの中に同じ数字は入らない

$\sum _{i \in \{ 0, 1, 2 \}} \sum _{j \in \{ 0, 1, 2 \}} x_{\text{r} + i, \text{c} + j, \text{num}} = 1, \hspace{10pt} \forall \text{r} \in \{ 1, 4, 7 \}, \text{c} \in \{ 1, 4, 7 \}, \text{num} \in \text{nums}$

制約条件⑤：既に数字が入っているマスは数字が固定

$x_{\text{row}, \text{col}, \text{num}} = 1, \hspace{10pt} \text{if} \hspace{5pt} \text{hint}_{\text{row}, \text{col}} \ne 0$

目的関数

数独の場合、目的関数は特にありません。

実装

今回実装したコードはGitHubでも公開しています。GitHubにはPuLPだけでなく、Python-MIPを使った実装も公開しています。

GitHub

参考サイト

GitHub - yshr10ic/optimization-practice: 数理最適化実践用リポジトリ

数理最適化実践用リポジトリ. Contribute to yshr10ic/optimization-practice development by creating an account on GitHub.

環境

Python：9.7.5
NumPy：1.24.1
PuLP：2.7.0

問題

わざわざクラスにする必要はありませんが、今回はクラスで実装してみました。

import numpy as np


class SudokuData:
    def __init__(self) -> None:
        self.hint = None

    def get_data(self) -> None:
        self.hint = np.array([
            [0, 0, 9, 0, 0, 8, 0, 0, 0],
            [1, 0, 6, 0, 9, 0, 0, 0, 0],
            [0, 0, 0, 0, 1, 0, 3, 0, 2],
            [0, 0, 0, 5, 7, 0, 0, 0, 0],
            [4, 3, 0, 0, 0, 0, 0, 0, 9],
            [0, 9, 8, 0, 0, 3, 0, 0, 0],
            [0, 0, 2, 0, 0, 0, 0, 7, 4],
            [6, 0, 0, 0, 0, 0, 8, 0, 0],
            [5, 4, 0, 0, 0, 0, 0, 0, 3]
        ])

答えがわかっていないマスは0としています。

数理最適化問題の定義

PuLPで数理最適化問題のベースとなるオブジェクトを生成します。

import pulp

model = pulp.LpProblem("Sudoku")

決定変数

次に決定変数 $x_{\text{row}, \text{col}, \text{num}}$ です。

PuLPではpulp.LpVariable.dictsを使用することで、for文を使うことなく多次元の決定変数を用意することができます。

rows = range(1, 10)
cols = range(1, 10)
nums = range(1, 10)

x = pulp.LpVariable.dicts("x", (rows, cols, nums), cat=pulp.LpBinary)

制約条件

制約条件①：各マスには必ず1〜9のいずれかの数字が入る

for row in rows:
    for col in cols:
        model += pulp.lpSum([x[row][col][num] for num in nums]) == 1

制約条件②：行方向に見た時に、同じ数字は入らない

for row in rows:
    for num in nums:
        model += pulp.lpSum([x[row][col][num] for col in cols]) == 1

制約条件③：列方向に見た時に、同じ数字は入らない

for col in cols:
    for num in nums:
        model += pulp.lpSum([x[row][col][num] for row in rows]) == 1

制約条件④：3×3のマスの中に同じ数字は入らない

for r in [1, 4, 7]:
    for c in [1, 4, 7]:
        for num in nums:
            model += pulp.lpSum([x[r+i][c+j][num] for i in range(3) for j in range(3)]) == 1

制約条件⑤：既に数字が入っているマスは数字が固定

for row in rows:
    for col in cols:
        if hint[row-1, col-1] != 0:
            model += x[row][col][hint[row-1, col-1]] == 1

目的関数

PuLPの場合、目的関数がない場合は0を代入します。

model += 0

求解

model.solve()

コード

数理最適化に関するコードをSudokuSolverクラスにまとめてみました。以下が最終的なコードです。

import numpy as np
import pulp


class SudokuData:
    def __init__(self) -> None:
        self.hint = None

    def get_data(self) -> None:
        self.hint = np.array([
            [0, 0, 9, 0, 0, 8, 0, 0, 0],
            [1, 0, 6, 0, 9, 0, 0, 0, 0],
            [0, 0, 0, 0, 1, 0, 3, 0, 2],
            [0, 0, 0, 5, 7, 0, 0, 0, 0],
            [4, 3, 0, 0, 0, 0, 0, 0, 9],
            [0, 9, 8, 0, 0, 3, 0, 0, 0],
            [0, 0, 2, 0, 0, 0, 0, 7, 4],
            [6, 0, 0, 0, 0, 0, 8, 0, 0],
            [5, 4, 0, 0, 0, 0, 0, 0, 3]
        ])


class SudokuSolver:
    def __init__(self, data: SudokuData, options: dict) -> None:
        self.hint = data.hint
        self.options = options

    def preprocess(self) -> None:
        pass

    def modeling(self) -> None:
        self.model = pulp.LpProblem("Sudoku")

        # 決定変数
        self.rows = range(1, 10)
        self.cols = range(1, 10)
        self.nums = range(1, 10)
        self.x = pulp.LpVariable.dicts("x", (self.rows, self.cols, self.nums), cat=pulp.LpBinary)

        # 制約条件
        ## 制約条件①：各マスには必ず1〜9のいずれかの数字が入る
        for row in self.rows:
            for col in self.cols:
                self.model += pulp.lpSum([self.x[row][col][num] for num in self.nums]) == 1

        ## 制約条件②：行方向に見た時に、同じ数字は入らない
        for row in self.rows:
            for num in self.nums:
                self.model += pulp.lpSum([self.x[row][col][num] for col in self.cols]) == 1

        ## 制約条件③：列方向に見た時に、同じ数字は入らない
        for col in self.cols:
            for num in self.nums:
                self.model += pulp.lpSum([self.x[row][col][num] for row in self.rows]) == 1

        ## 制約条件④：3×3のマスの中に同じ数字は入らない
        for r in [1, 4, 7]:
            for c in [1, 4, 7]:
                for num in self.nums:
                    self.model += pulp.lpSum([self.x[r+i][c+j][num] for i in range(3) for j in range(3)]) == 1

        ## 制約条件⑤：既に数字が入っているマスは数字が固定
        for row in self.rows:
            for col in self.cols:
                if self.hint[row-1, col-1] != 0:
                    self.model += self.x[row][col][self.hint[row-1, col-1]] == 1

        # 目的関数
        self.model += 0

        # 求解
        self.model.solve(pulp.PULP_CBC_CMD(**self.options))

    def postprocess(self):
        self.solution = np.empty((9, 9))
        for row in self.rows:
            for col in self.cols:
                for num in self.nums:
                    val = self.x[row][col][num].value()
                    if val == 1:
                        self.solution[row-1, col-1] = num
        self.solution = self.solution.astype(int)


if __name__ == "__main__":
    sudoku_data = SudokuData()
    sudoku_data.get_data()

    # PuLPのログ出力をオフにし、求解の上限時間をなしに設定
    options = dict(
        msg=0,
        timeLimit=None,
    )

    solver = SudokuSolver(sudoku_data, options=options)
    solver.preprocess()
    solver.modeling()
    solver.postprocess()

実行結果はこのようになりました。問題なく解けていますね！

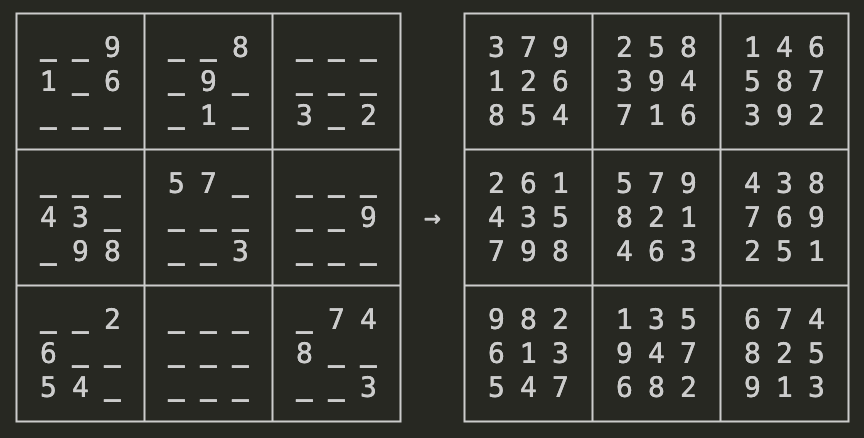
まとめ

今回は混合整数計画問題をモデリングするためのPythonライブラリであるPuLPを用いて、数独を解いてみました。次回はGoogle OR-ToolsのCP-SAT Solverを用いて、制約プログラミングで数独を解いてみたいと思います。

数理最適化を勉強するのにおすすめな書籍

Pythonではじめる数理最適化 ―ケーススタディでモデリングのスキルを身につけよう―

created by Rinker

しっかり学ぶ数理最適化　モデルからアルゴリズムまで (ＫＳ情報科学専門書)

created by Rinker

¥3,300
(2024/09/11 03:16:07時点 Amazon調べ-詳細)

あたらしい数理最適化: Python言語とGurobiで解く

created by Rinker

¥3,168
(2024/09/11 23:20:21時点 Amazon調べ-詳細)

PuLP Python やってみた数独数理最適化

数理最適化で数独を解いてみた（PuLP編）

今回解く数独の定義

定式化

決定変数

制約条件

制約条件①：各マスには必ず1〜9のいずれかの数字が入る

制約条件②：行方向に見た時に、同じ数字は入らない

制約条件③：列方向に見た時に、同じ数字は入らない

制約条件④：3×3のマスの中に同じ数字は入らない

制約条件⑤：既に数字が入っているマスは数字が固定

目的関数

実装

環境

問題

数理最適化問題の定義

決定変数

制約条件

制約条件①：各マスには必ず1〜9のいずれかの数字が入る

制約条件②：行方向に見た時に、同じ数字は入らない

制約条件③：列方向に見た時に、同じ数字は入らない

制約条件④：3×3のマスの中に同じ数字は入らない

制約条件⑤：既に数字が入っているマスは数字が固定

目的関数

求解

コード

まとめ

数理最適化を勉強するのにおすすめな書籍

【Notionで実験管理】Google ColabからNotionに実験結果を連携する

【山善】電動昇降式デスクを買いました！！！